Multiple Linear Regression

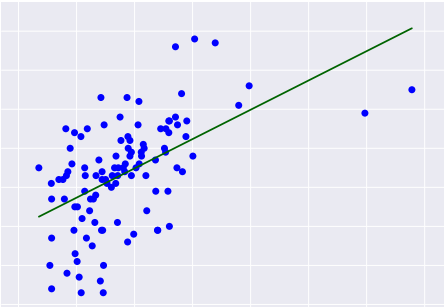
Multiple Linear Regression (MLR) is a foundational statistical technique used to model the relationship between a dependent variable and multiple independent variables. This approach extends simple linear regression by incorporating several predictors, allowing for a more nuanced understanding of how various factors influence outcomes.

The MLR model is typically expressed by the equation:

Where:

• Y represents the dependent variable that we aim to predict.
• β0​ is the intercept, the expected value of $Y$ when all $X$ values are zero.
• β1​, β2​,…,βn​ are the coefficients of the independent variables $X_1, X_2, \dots, X_n$, representing the change in $Y$ for a one-unit change in each $X$
• $$ϵ is the error term, capturing unobserved factors influencing $Y$

$\mathrm{<br>}$

Key Principles and Assumptions of MLR

1. Linearity: The relationship between the dependent and independent variables is assumed to be linear.
2. Independence: Observations must be independent, ensuring the validity of test statistics.
3. Homoscedasticity: The variance of error terms should be constant across all levels of independent variables.
4. Normality: Residuals (the differences between observed and predicted outcomes) should be normally distributed.
5. Multicollinearity: Independent variables should not be highly correlated with each other, as this can inflate the variance in coefficient estimates.
   
   

MLR in Python

# Load the dataset
data = pd.read_csv('your_dataset.csv')

# Define the features and target variable
X = data[['feature1', 'feature2', 'feature3']]
y = data['target']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Fit the model
model = LinearRegression()
model.fit(X_train, y_train)

# Make predictions
predictions = model.predict(X_test)

# Calculate mean squared error
mse = mean_squared_error(y_test, predictions)
print('Mean Squared Error:', mse)

# Print the coefficients
print('Coefficients:', model.coef_)

Overview

The Python code provided here demonstrates how to perform Multiple Linear Regression using the scikit-learn library. Multiple Linear Regression is a statistical technique used to understand the relationship between multiple independent variables (features) and a dependent variable (target).

Usage Instructions

1. Replace 'your_dataset.csv' with the filename of your dataset containing the relevant data for the regression analysis.
2. Replace 'feature1', 'feature2', 'feature3', and 'target' with the actual column names representing the independent features and the dependent target variable in your dataset.
3. Ensure that the dataset is in CSV format and accessible from the same directory as your Python script.
4. Run the script in a Python environment that has the required libraries installed (pandas, numpy, scikit-learn).

Code Explanation

1. Import Libraries: The code imports necessary libraries: pandas, numpy, LinearRegression, train_test_split, and mean_squared_error from scikit-learn.
2. Load Dataset: The code loads the dataset from the specified CSV file.
3. Define Features and Target: The code selects the relevant features ('feature1', 'feature2', 'feature3') and the target variable ('target') from the dataset.
4. Split Data: The code splits the dataset into training and testing sets using the train_test_split function.
5. Fit the Model: A Linear Regression model is instantiated and trained with the training data using the fit method.
6. Make Predictions: The model makes predictions on the test data using the predict method.
7. Calculate Mean Squared Error: The code calculates the mean squared error between the actual target values and the predicted values.
8. Display Results: The mean squared error is printed to the console.

Note

• Ensure that the dataset contains numerical data for features and the target variable.

• It is recommended to preprocess the data (e.g., handling missing values, scaling features) before performing regression analysis.

• Consider further evaluation metrics and visualization techniques to analyze the performance of the model.

By following the instructions and understanding the code's execution flow, you can utilize this script to perform Multiple Linear Regression on your dataset effectively.

MLR in R

# Fit the Multiple Linear Regression Model:
data <- read.csv("data.csv")
# Fit the Multiple Linear Regression Model:
model <- lm(Y ~ X1 + X2 + X3, data=data)
# Print the summary of the model
summary(model)

Usage Instructions

To run a multiple linear regression analysis using the provided code:

1. Ensure that your dataset is stored in a CSV file named "data.csv".
2. Replace 'Y' with the name of your dependent variable and 'X1', 'X2', 'X3' with the names of your independent variables in the 'lm' function.
3. Execute the code in an R environment to fit the regression model and view the summary results.

By following these steps, you can perform a multiple linear regression analysis using R with the provided code.

Code Explanation

1. Load the Dataset: This line of code reads the dataset from a CSV file named "data.csv" and stores it in the variable 'data'.

2. Fit the Multiple Linear Regression Model: This code fits a multiple linear regression model using the 'lm' function where Y is the dependent variable and X1, X2, and X3 are independent variables from the dataset 'data'.

3. Print Model Summary: This line of code prints a summary of the fitted regression model, including coefficients, standard errors, t-values, and p-values for each independent variable.

Multiple Linear Regression is a cornerstone of predictive analytics and can be a great way to find and interpret patterns in data.

For more in-depth information, check out the following free, online resources:

• https://www.statology.org/multiple-linear-regression/ 
• https://statisticsbyjim.com/regression/linear-regression/ 
• https://www.youtube.com/watch?v=dQNpSa-bq4M 
• https://www.youtube.com/watch?v=lng4ZgConCM